Research
My research vision is to equip robots with certifiably optimal and safe behavior, enabling their seamless integration into complex and dynamic environments shared with humans.
My research focus to date has been on the aspect of safe spatial perception, which I believe is the fundamental enabler for all complex tasks that robots need to solve. An important aspect of safety in spatial perception is being able to certify the quality of solutions to non-convex optimization problems, which we have addressed in our latest stream work works on global optimality for state estimation. Another important aspect is safe operation in the event of sensor degradation, to which I have contributed during my PhD using unconventional, non-visual measurement modalities for spatial perception, such as Bluetooth, WiFi, Ultra-Wideband (UWB) and sound, thus increasing the resilience of robots to the failure of one or more sensing modalities.
More broadly speaking, I am interested in applied mathematics and formal guarantees for robotics, and the interplay between model-based and data-driven approaches for safe autonomy.
Current research
Global optimization for robotics with unknown models
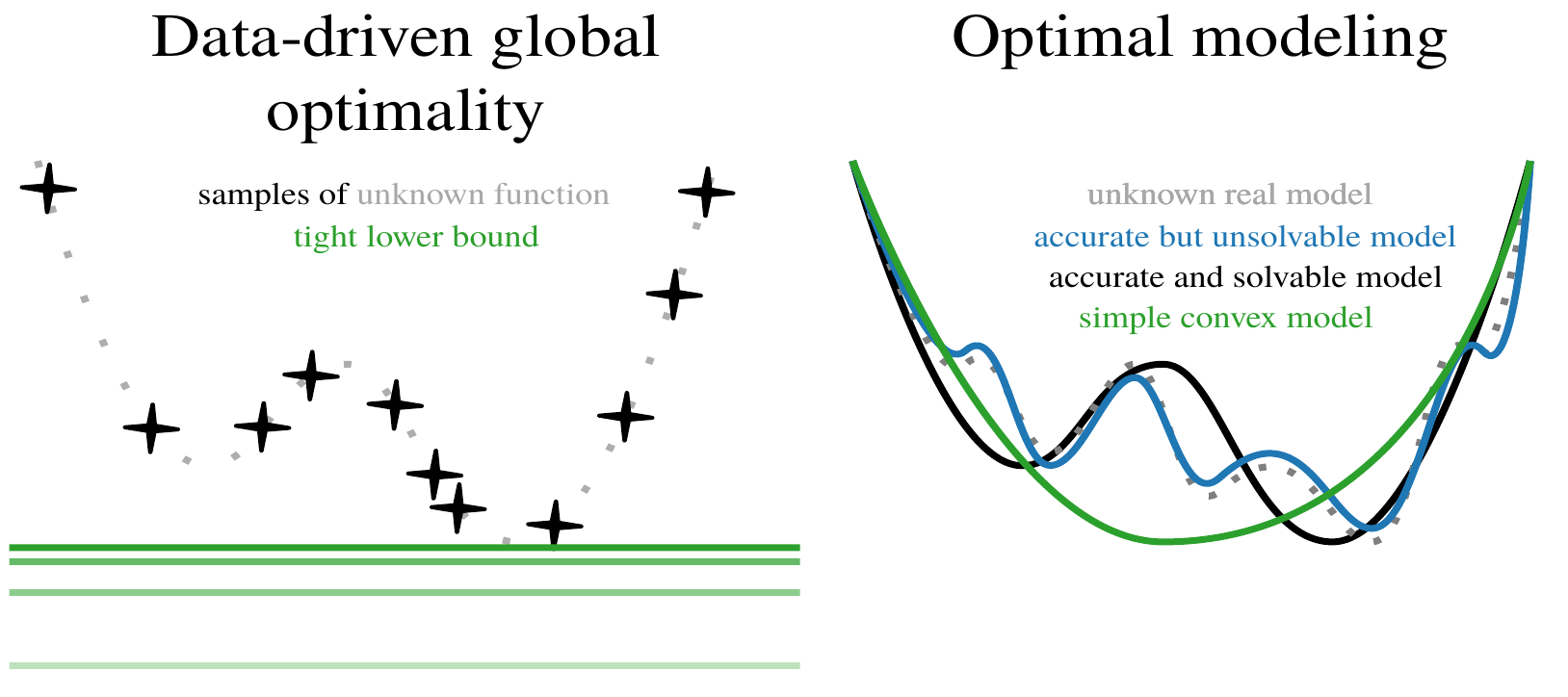
Recent work in robotics has shown that many classical state estimation problems can be formulated as polynomial problems with tight semidefinite relaxations. This means that the global minimum can often be found by just solving one convex problem (usually a semidefinite program). I have explored instances of this methodology in past and ongoing research, described in the section below.
In this research project, I am exploring two follow-up questions. First, how can we find globally optimal solutions to problems where the model may be inaccurate, only partially (or not at all) known, or when we have no tractable state representation (think cloth or grains)? Answering this question will unlock many new application areas for globally optimal methods; including planning through contact, safe control of poorly calibrated systems, and efficient manipulation of soft and uncountable objects. Second, I explore how to learn optimal models from data; using ingredients such as differentiable optimization to find models that are adapted to the task of interest. This research directly spawns many interesting subproblems, such as active perception to learn models from less data, online adaptation of model estimates, and their global optimality.
Certifiable state estimation
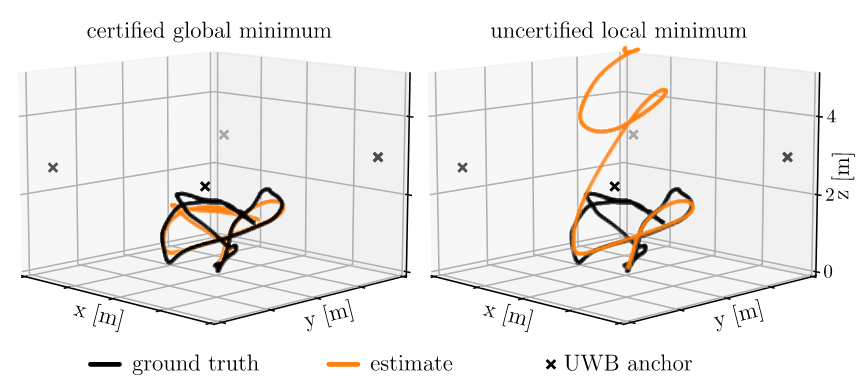
Common solvers used in robotics state estimation, such as Gauss-Newton or Levenberg-Marquardt, provide first-order optimal solutions very reliably. Because most optimization problems encountered in robotics are non-convex, these solutions may however correspond to local optima, and may be far from the global optimum. In this research project we are exploring ways to ensure the quality of candidate solutions, exploiting concepts from Lagrangian duality theory. An accessible introduction to this topic is given in our arXiv paper on robust line fitting.
A summary of the work we did in this area was presented at the R:SS 2024 Workshop on Safe Autonomy, available here, under the extending the catalogue section. In summary, we created novel certifiably optimal solvers for a variety of state estimation problems; including the non-linear and typically underdetermined range-only localization, localization from non-isotropic measurements, common in stereo-camera observations, and finally, rotation and pose averaging and synchronization from rotation measurements, using the Cayley map to maintain polynomial problem formulations.
Past research
Acoustic echolocation for small robots
We have investigated ways to use audio signals for localization and mapping on small robots, getting rid of the commonly placed requirement for high-quality measurement microphones and powerful speakers, and replacing it with more commonly available MEMS microphones and little alarm-like buzzers. Our research shows that walls can be reliably detected and avoided, based on sound only, on small robots such as the Crazyflie drone, a developer-friendly nano drone, and the e-puck2 education robot. For this purpose, we have built a custom extension deck with microphones and a buzzer for the Crazyflie drone, thus emulating a “bat drone”. More details are available in our paper (also available on arXiv), published in RA-L 2022 and presented at IROS 2022 in Kyoto, and in our blogpost on the Crazyflie website.
Indoor localization
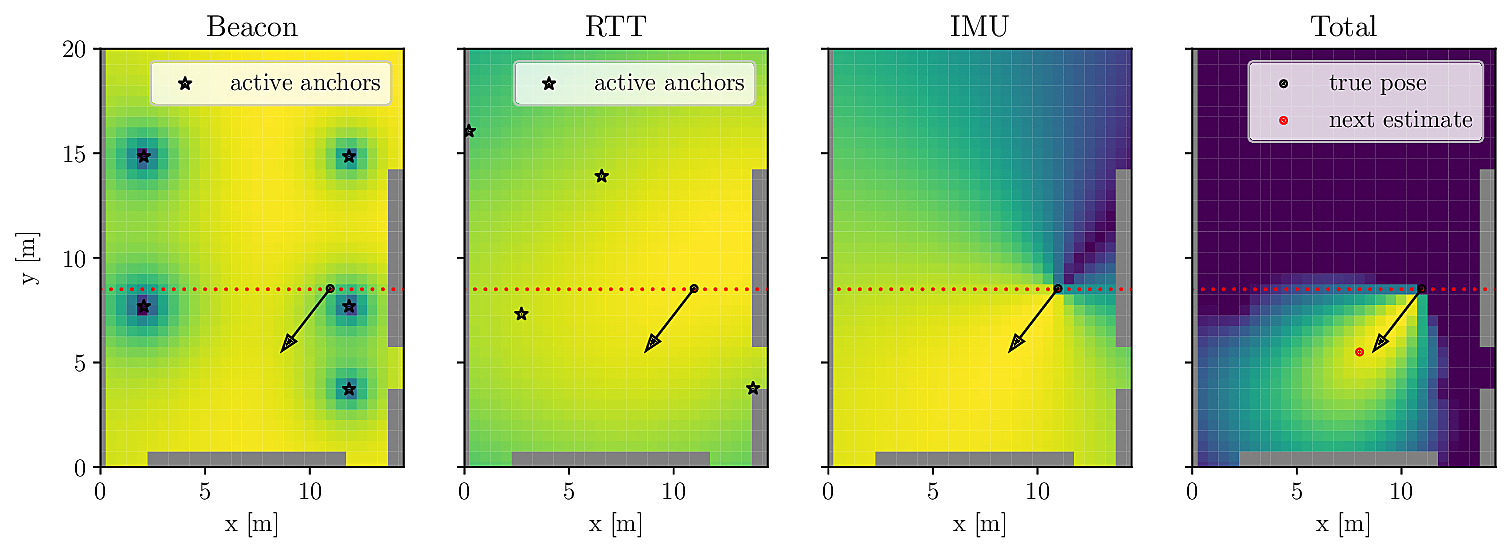
We have created a smartphone-compatible indoor localization solution based on Bluetooth signal strength, WiFi round-trip-time, inertial measurement unit signals, and occasional camera images. This project was a collaboration with the School of Engineering and Architecture of Fribourg and Vidinoti, a company providing Augmented Reality solutions. Our method, presented at IPIN2019, does not require prior calibration or fingerprinting, while maintaining meter-level accuracy.
Computer Vision
Since my Master’s thesis at the Autonomous Systems Lab, I have been interested in computer vision, in particular in 3D reconstruction. I had the chance to work on this topic again during an internship at Disney Research in Los Angeles, which resulted in this paper and a U.S. patent. Besides that, I had three projects with my colleagues from IVRL: a project on image dehazing, a tutorial paper on Fourier deconvolution, and a project on a novel activation loss for convolutional neural networks.
Coordinate Difference Matrices
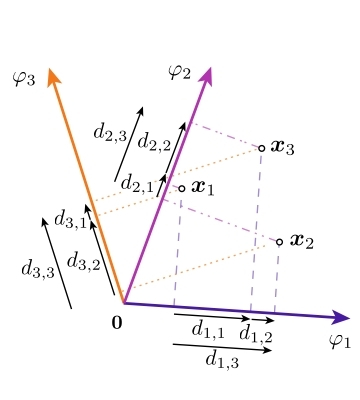
We have conducted a group project over several years on vector geometry problems. We coined the term Coordinate Difference Matrices, mathematical objects closely related to Euclidean Distance Matrices, which exhibit some interesting mathematical properties. These properties can be exploited in various active research domains, such as the molecular conformation problem, multi-modal localization and microphone array calibration.